从薛定谔方程的问世开始，第一性原理电子结构计算就成为了自然科学研究的重要方法，尤其是对物理学、化学和材料学的研究起到了重要的推动作用。对物质电子结构的精确求解意味着人们可以预测基于电磁相互作用力的系统的宏观性质，因此，基态波函数能够表征一个体系最根本的性质，是发展电子结构计算方法的重中之重。其中变分蒙特卡洛（Variational Monte Carlo, VMC）和扩散蒙特卡洛（diffusion Monte Carlo, DMC）等量子蒙特卡洛（Quantum Monte Carlo, QMC）方法是电子结构计算方法中最精确的代表者之一。然而，传统的VMC方法和DMC方法都有局限性，前者结果严重依赖于人为设定的波函数拟设，后者则受困于“符号问题”导致的试探波函数的节点问题。近些年，得益于深层神经网络等机器学习技术的发展，采用神经网络作为多体电子波函数的拟设并结合VMC的电子结构计算方法展现出了非常强的潜力，是一种能够通过非监督式机器学习逐渐逼近多电子体系基态的方法。然而，神经网络庞大的参数量带来的漫长收敛过程和昂贵计算代价使得机器学习量子蒙特卡洛在大型体系上的应用依然具有巨大的挑战性。

近日，6163银河线路检测中心凝聚态物理与材料物理研究所陈基研究员课题组与字节跳动研究部任维络博士等合作，将深度学习神经网络波函数方法与DMC方法相结合，开发了一个新的GPU友好、可高度并行化的神经网络DMC方法，大幅提升了分子体系电子结构总能计算的精度（图1）。相关研究成果以“以神经网络扩散蒙特卡洛逼近分子基态”（Towards the ground state of molecules via diffusion Monte Carlo on neural networks）为题，在线发表于《自然·通讯》（Nature Communications 2023, 14, 1860）。

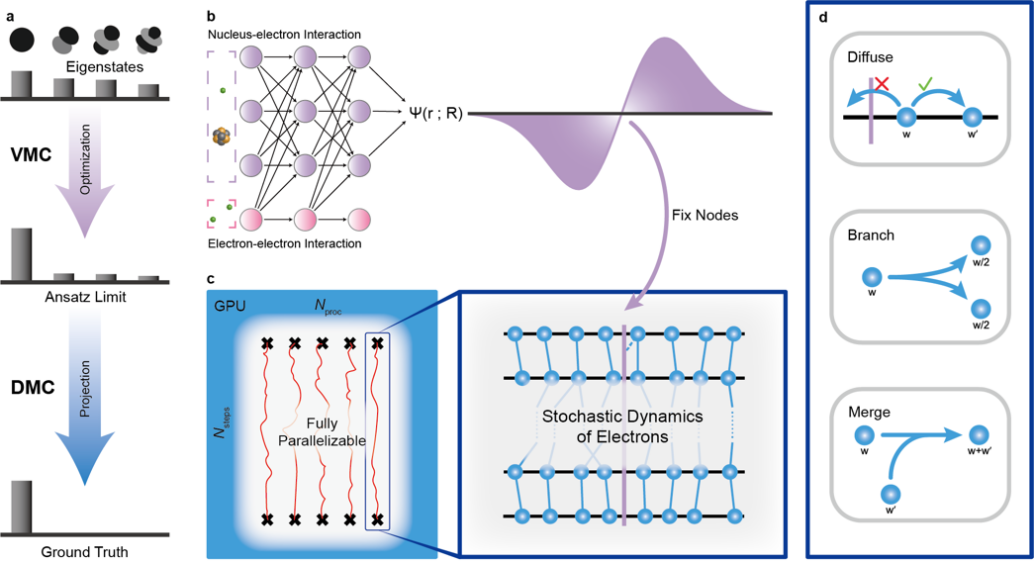
图1.a, VMC方法可以将波函数优化至接近基态，但由于函数模型表达能力有限，其精度存在一个上限。DMC方法通过虚时演化的方法将波函数向基态投影从而得以突破这一精度上限。b,构建一个满足费米子交换反对称性的神经网络函数模型从而可以表示多体电子波函数。c, GPU友好、可高度并行化的DMC算法以及算法中游走子的随机扩散动力学简单示意图。d, DMC算法中的三个重要步骤：游走子的扩散、繁衍和湮灭。

图2展示了神经网络DMC计算在一系列体系上的结果的优越性。神经网络DMC方法在效率、精度上相较于已有方法均有着较大的提升。在氮气、环丁二烯、水二聚物团簇等一系列具有挑战性的分子体系上比最精确的量子化学方法更准确，能够非常好的符合实验结果。此外，该工作是领域内首个用神经网络QMC方法对苯环二聚体这个规模的分子体系进行计算的工作。苯环二聚体的结合能是标定电子结构计算方法精度的一个重要体系，神经网络DMC方法相比于VMC等方法进步显著。

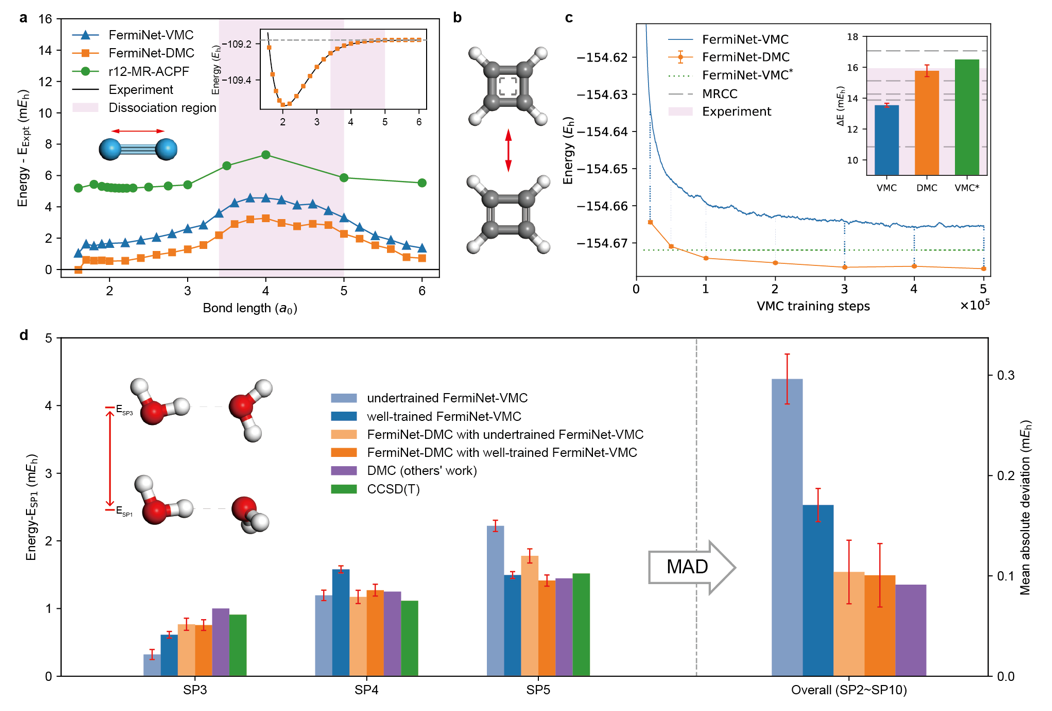
图2.各类体系上的计算结果展示。a,氮气分子的计算结果，其中蓝线为神经网络VMC方法，橙线为神经网络DMC方法，绿线为该体系上最精确的量子化学方法。b,环丁二烯的平衡态构型（下）和过渡态构型（上）。c,环丁二烯的平衡态构型计算曲线（主图）和转变势垒计算结果（小图）。d,水二聚物团簇的不同方法计算结果。

该工作中实现的神经网络DMC方法对于研究凝聚态物理中的电子关联问题、复杂材料的电子结构以及精准量子化学等具有重要的意义，将成为电子结构计算领域新的标杆式计算方法。此项研究是合作研究团队在发展机器学习QMC算法的系列工作中的又一重要进展。此前，双方已先后合作开发了机器学习QMC方法中的原子有效核势（Phys. Rev. Research 2022, 4, 013021）；实现了机器学习QMC方法中原子间作用力的计算（J. Chem. Phys. 2022, 157, 164104）；开发了领域内首个适用于研究固体等周期性体系的神经网络波函数模型DeepSolid（Nature Communications 2022, 13, 7895）。未来，将神经网络DMC方法与已经开发的这些方法相结合可以进一步提高各类体系的计算精度。

任维络和6163银河线路检测中心2021级博士生付伟中是本文的共同第一作者，任维络和陈基是文章的共同通讯作者，文章作者还包括字节跳动研究部吴小杰博士。陈基课题组的工作得到了国家重点研发计划、国家自然科学基金、中国科学院战略性先导科技专项的支持。

原文链接：https://www.nature.com/articles/s41467-023-37609-3